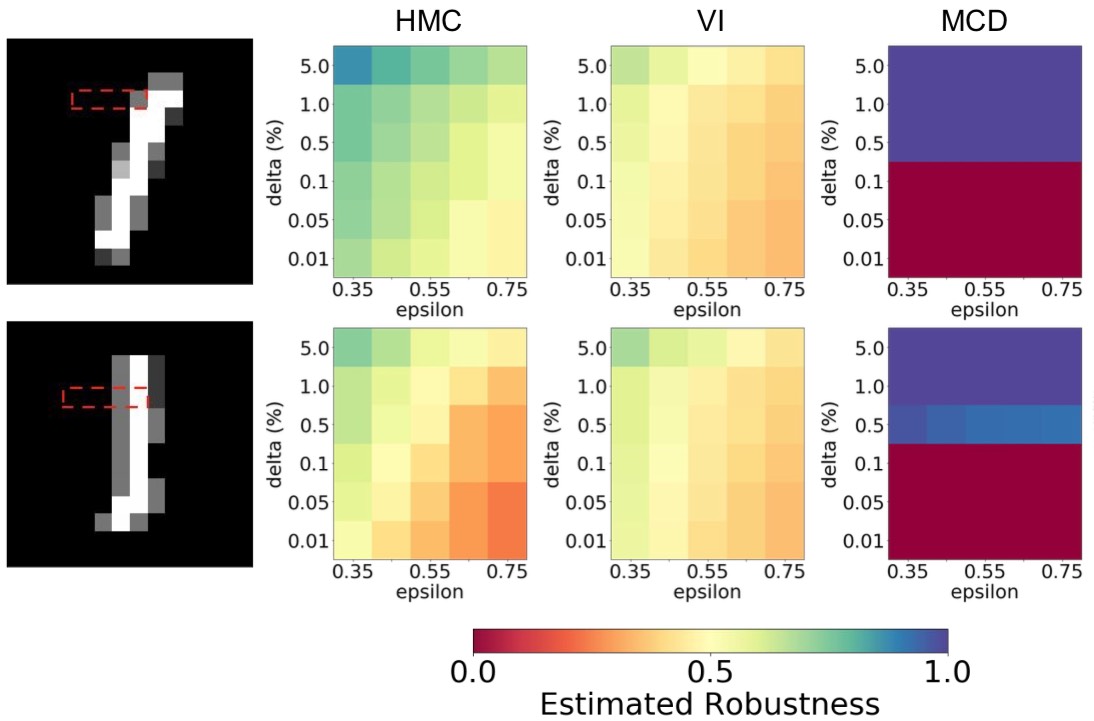
We introduce a probabilistic robustness measure for Bayesian Neural Networks (BNNs), defined as the probability that, given a test point, there exists a point within a bounded set such that the BNN prediction differs between the two. Such a measure can be used, for instance, to quantify the probability of the existence of adversarial examples. Building on statistical verification techniques for probabilistic models, we develop a framework that allows us to estimate probabilistic robustness for a BNN with statistical guarantees, i.e., with a priori error and confidence bounds, by leveraging a sequential probability estimation scheme based on the Massart bounds.

We evaluate our method with several approximate BNN inference techniques on image classification tasks associated to the MNIST digit recognition dataset and a two-class subset of the German Traffic Sign Recognition Benchmark (GTSRB) dataset, showing that the method enables quantification of uncertainty of BNN predictions in adversarial settings. Code available in GitHub.

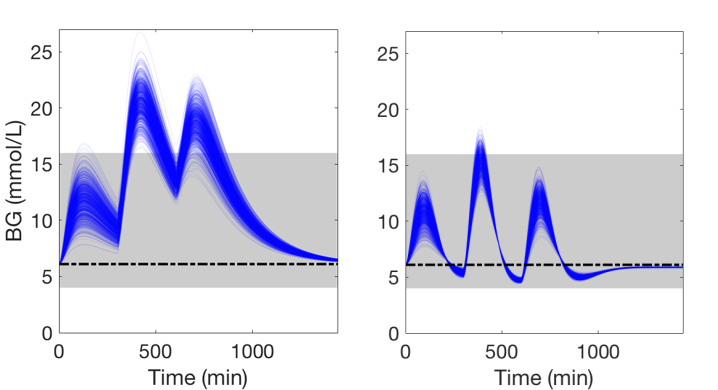
The artificial pancreas aims to automate treatment of type 1 diabetes (T1D) by integrating insulin pump and glucose sensor through control algorithms. However, fully closed-loop therapy is challenging since the blood glucose levels to control depend on disturbances related to the patient behavior, mainly meals and physical activity.

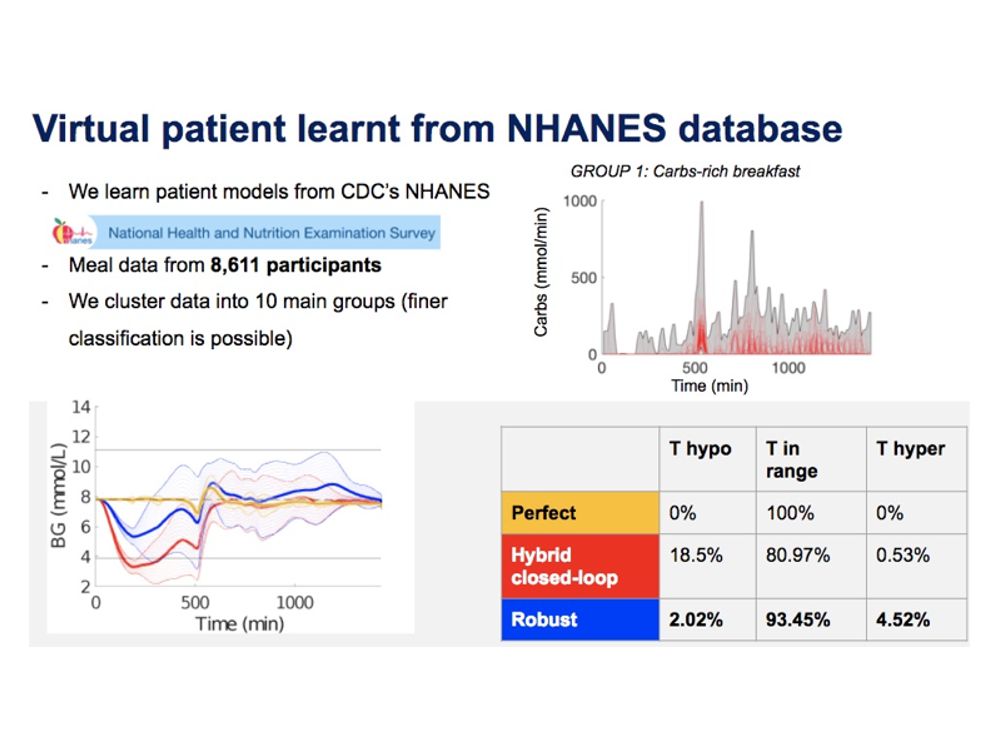
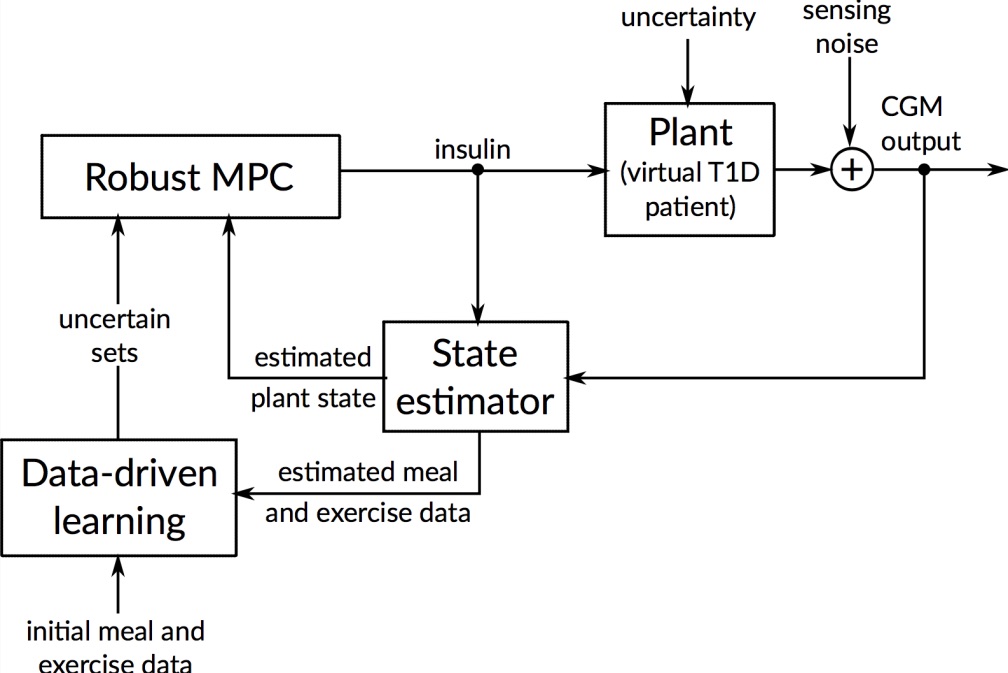
To handle meal and exercise uncertainties, in our work we construct data-driven models of meal and exercise behavior, and develop a robust model-predictive control (MPC) system able to reject such uncertainties, in this way eliminating the need for meal announcements by the patient. The data-driven models, called uncertainty sets, are built from data so that they cover the underlying (unknown) distribution with prescribed probabilistic guarantees. Then, our robust MPC system computes the insulin therapy that minimizes the worst-case performance with respect to these uncertainty sets, so providing a principled way to deal with uncertainty. State estimation follows a similar principle to MPC and exploits a prediction model to find the most likely state and disturbance estimate given the observations.

We evaluate our design on synthetic scenarios, including high-carbs intake and unexpected meal delays, and on large clusters of virtual patients learned from population-wide survey data sets (CDC NHANES).

We present a new method for the automated synthesis of digital controllers with formal safety guarantees for systems with nonlinear dynamics, noisy output measurements, and stochastic disturbances. Our method derives digital controllers such that the corresponding closed-loop system, modeled as a sampled-data stochastic control system, satisfies a safety specification with probability above a given threshold. The method alternates between two steps: generation of a candidate controller (sub-optimal but rapid to generate), and verification of the candidate. The candidate is found by maximizing a Monte Carlo estimate of the safety probability, and by simulating the system with a non-validated ODE solver. To rule out unstable candidate controllers, we prove and utilize Lyapunov indirect method for instability of sampled-data nonlinear systems. In the verification step, we use a validated solver based on SMT to compute a numerically and statistically valid confidence interval for the safety probability of the candidate controller. If such probability is not above the threshold, we expand the search space for candidates by increasing the controller degree. We evaluate our technique on three case studies: an artificial pancreas model, a powertrain control model, and a quadruple-tank process.

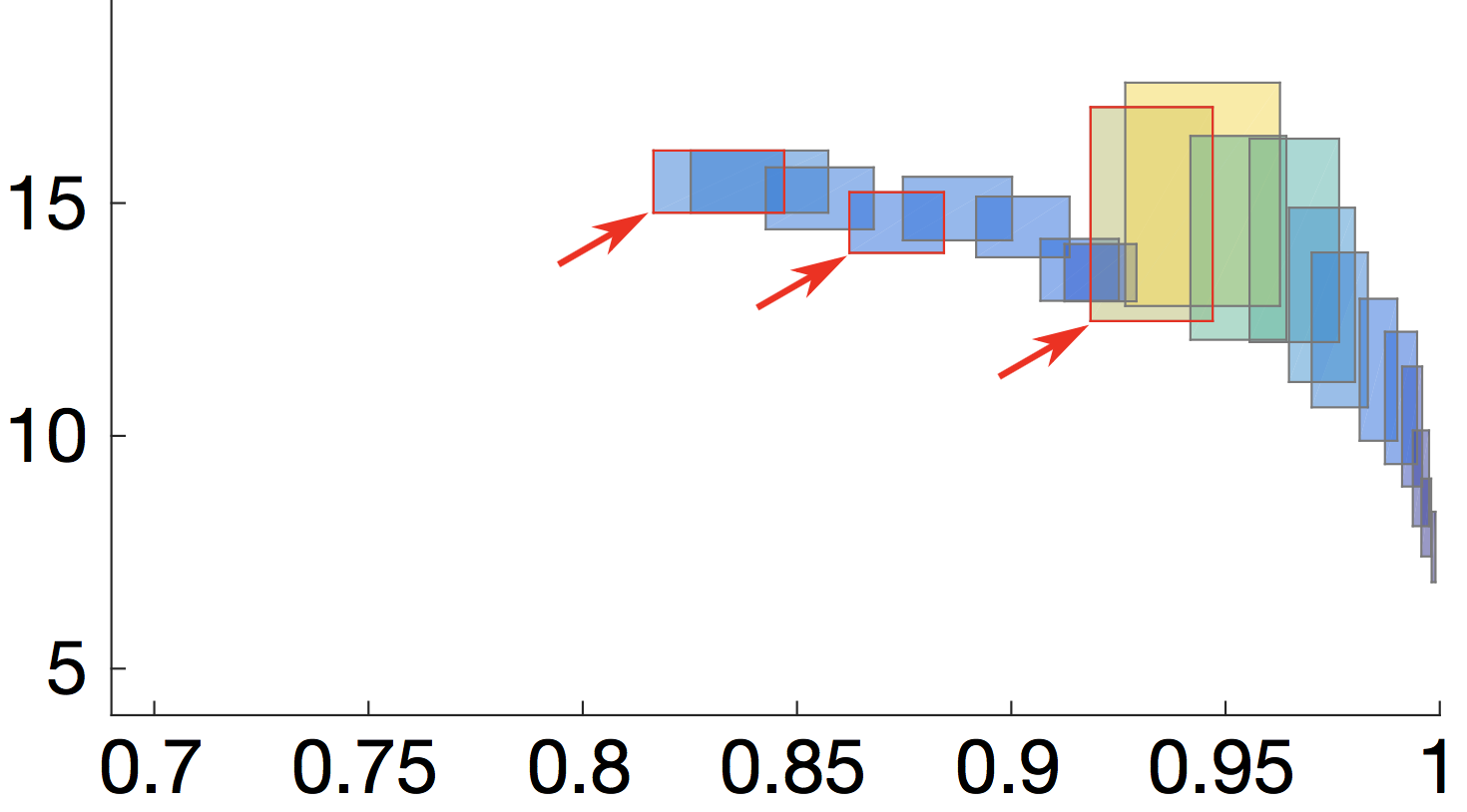
We consider the problem of synthesizing optimal and robust designs (given as parametric Markov chains) that are 1) robust to pre-specified levels of variation in the system parameters; 2) satisfy strict performance, reliability and other quality constraints; and 3) are Pareto optimal with respect to a set of quality optimisation criteria.

The resulting Pareto front consists of quality attribute regions induced by the parametric designs (see picture). The size and shape of these regions provide key insights into the system robustness since they capture the sensitivity of quality attributes to parameter changes (i.e, small regions = robust designs).

The method is implemented in the RODES tool and is based on a combination of GPU-accelerated parameter synthesis for Markov chains (to compute the quality attribute regions for fixed discrete parameters) through the PRISM-PSY tool, and multi-objective optimization based on an extended, sensitivity-aware dominance relation.